Kaosun Haritası: Ayrık Zamanlı Dinamik Sistemlere Giriş

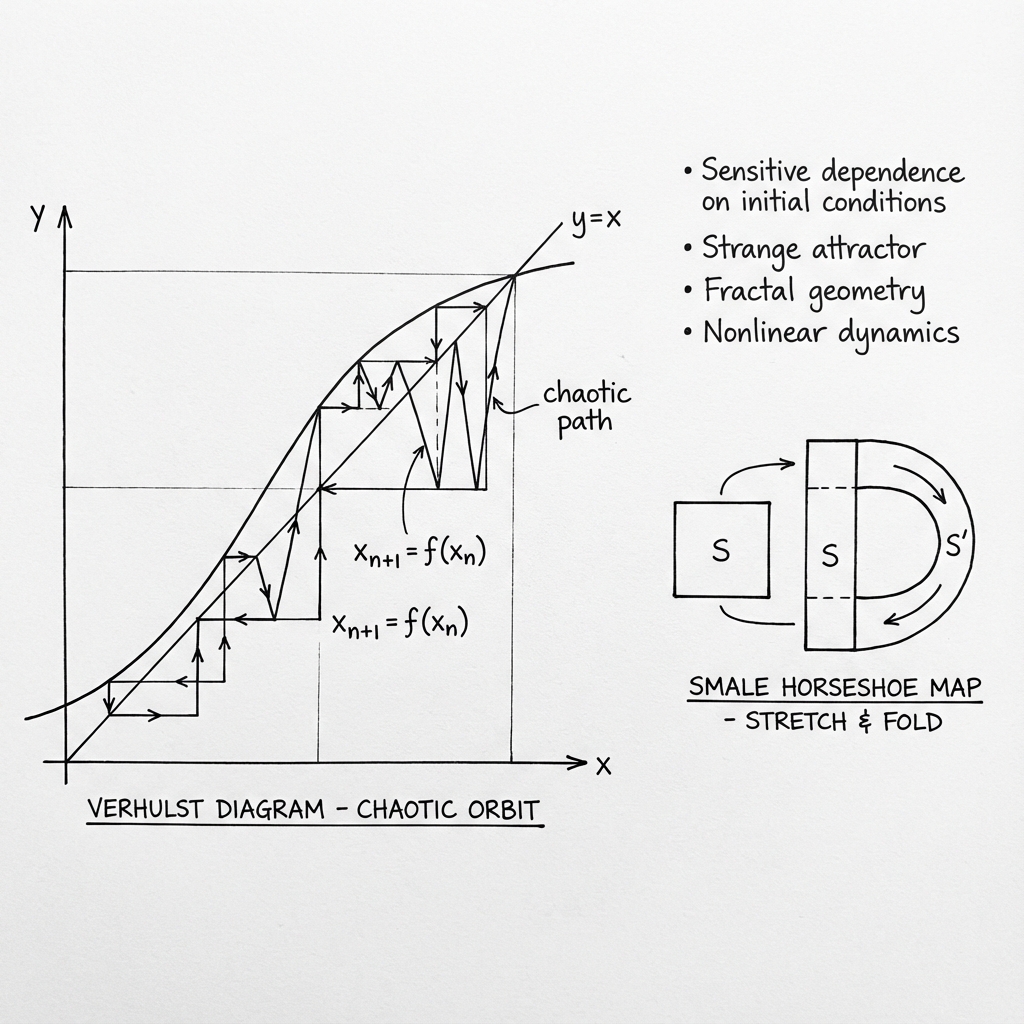Yukarıdaki mühendislik çizimi, lojistik harita üzerindeki kaotik yörüngeleri (örümcek ağı diyagramı) ve Smale at nalı haritasındaki esneme-katlanma (stretch & fold) mekanizmasını görselleştirmektedir.

Özet: Kaos teorisi denildiğinde aklımıza genellikle “kelebek etkisi” veya rastgelelik gelir. Ancak kaosun matematiği, şaşırtıcı derecede düzenli kurallar ve belirgin yapılar üzerine kuruludur. Bu yazıda, karmaşık diferansiyel denklemlerden (sürekli zaman) uzaklaşıp, kaosun temel yapı taşı olan Ayrık Zamanlı Dinamik Sistemleri inceleyeceğiz.

Bir fonksiyonun içine bir sayı atıp, çıkan sonucu tekrar aynı fonksiyona soktuğumuzda ne olur? Gelin, bu basit sorunun bizi nasıl karmaşık “yörüngelere” götürdüğüne bakalım.

1. Temel Mekanizma: Döngüler ve Yörüngeler

Dinamik sistemleri anlamak için önce “ayrık haritalama” kavramını oturtmamız gerekir. Elimizde tek boyutlu bir $f(x)$ fonksiyonu olduğunu düşünün. Bu fonksiyonu bir sayı dizisi oluşturmak için kullanacağız.

Süreç, bilgisayar programlamadaki bir “for döngüsü” veya “yineleme” mantığıyla çalışır:

1. Bir başlangıç noktası ($x_0$) seçersiniz.
2. Bu sayıyı fonksiyona koyarsınız: $x_1 = f(x_0)$.
3. Çıkan sonucu tekrar fonksiyona koyarsınız: $x_2 = f(x_1)$.

Bu işlem sonsuza kadar devam eder ve ${x_0, x_1, x_2, …}$ şeklinde giden bir sayı dizisi oluşturur. İşte bu diziye o noktanın Yörüngesi denir. Dinamik sistemlerin temel amacı, bu yörüngenin uzun vadede nereye gittiğini (limitlerini) anlamaktır. Sonsuza mı gidiyor? Bir noktada duruyor mu? Yoksa kaosun içinde savruluyor mu?

Eğer fonksiyonumuzun tersi alınabiliyorsa ($f$ invertible ise), geçmişe doğru giderek bir “geriye dönük yörünge”den de bahsedebiliriz. Ancak kaos teorisinde inceleyeceğimiz basit ama ilginç sistemlerin çoğu tersinebilir değildir.

Kaos İçin Bir Analoji: Hamur Yoğurmak Basit kaosu bir hamur yoğurma süreci gibi düşünebilirsiniz. Hamuru önce uzatırsınız, sonra kendi üzerine katlarsınız. Bu katlama işlemi yüzünden, hamurun şu anki haline bakarak geçmişte hangi parçanın nerede olduğunu kesin olarak bilmek zorlaşır (tersinebilirlik kaybı). Dinamik sistemlerdeki kaos da uzaydaki noktaları sürekli esnetip katlayarak karıştırır.

2. Sabit Noktalar ve Periyodik Davranışlar

Bir sistemi analiz ederken ilk bakacağımız yerler, sistemin durduğu veya tekrar ettiği noktalardır.

Sabit Noktalar

Eğer bir sayıyı fonksiyona koyduğunuzda size aynı sayıyı geri veriyorsa, o bir sabit noktadır. Denklemi şöyledir:

Bu noktadan başlarsanız, yörüngeniz ${x, x, x, …}$ şeklinde sabit bir dizi olur.

Örnek: $f(x) = x^3$ fonksiyonunu ele alalım. Bu fonksiyonun sabit noktalarını bulmak için $x^3 = x$ denklemini çözeriz. Çözümler $0, 1$ ve $-1$’dir. Bu noktalardan başlarsanız sistem asla hareket etmez.

Periyodik Noktalar

Bazı noktalar hemen kendine dönmez, ancak belirli bir adım sayısından sonra başlangıç konumuna geri gelir. Eğer $p$ adım sonra geri geliyorsa buna periyodik nokta denir:

Burada “Asal Periyot”, tekrarın gerçekleştiği en küçük $p$ değeridir.

Örnek: $f(x) = x^2 - 1$ fonksiyonuna bakalım. Eğer $x = 0$ ile başlarsanız:

• $0 \to -1$ (çünkü $0^2 - 1 = -1$)
• $-1 \to 0$ (çünkü $(-1)^2 - 1 = 0$) Yörünge ${0, -1, 0, -1…}$ şeklinde devam eder. Bu, asal periyodu 2 olan bir yörüngedir.

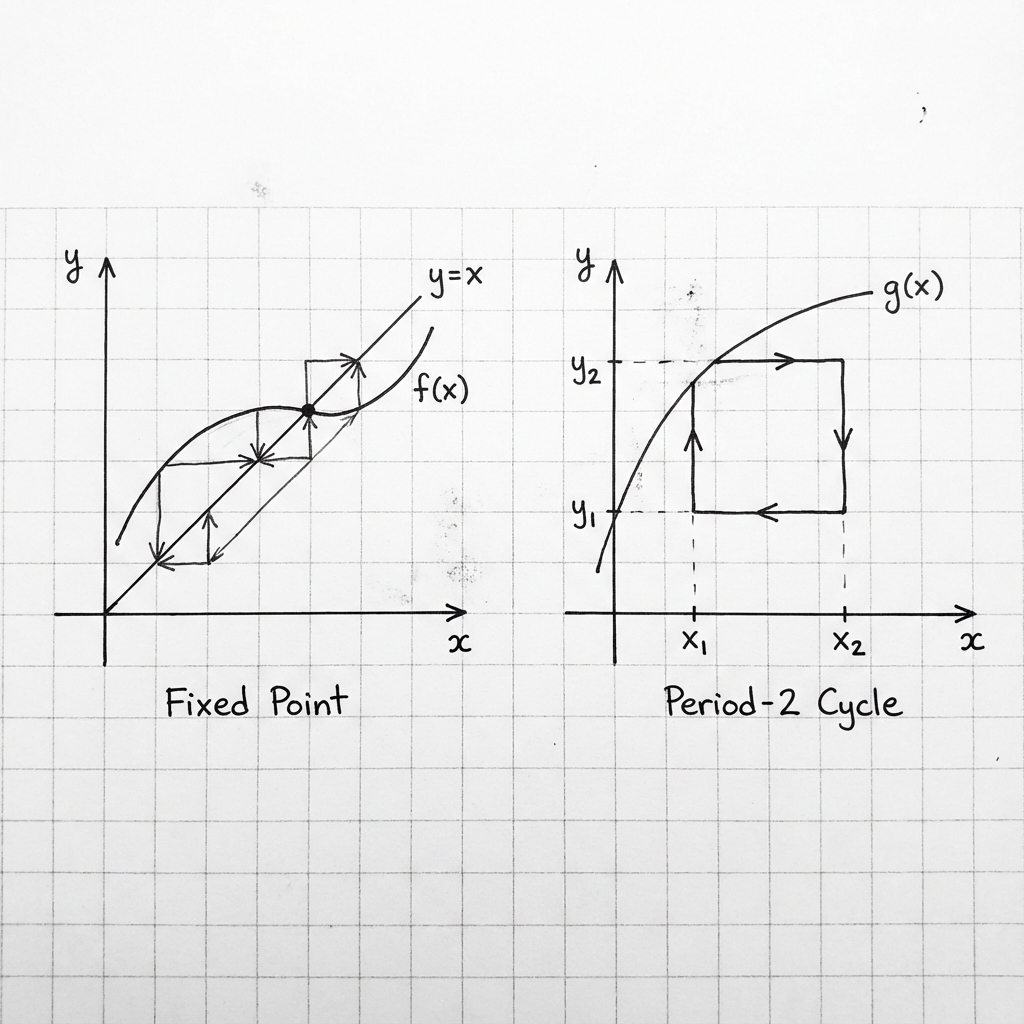Sol: Sabit bir noktaya yakınsayan yörünge. Sağ: İki nokta arasında gidip gelen periyodik döngü.

Ayrıca Ön-Periyodik noktalardan da bahsedebiliriz. Örneğin $f(x) = x^2$ fonksiyonunda $-1$ noktasından başlarsanız, bir adım sonra $1$’e gidersiniz ve orada sonsuza kadar kalırsınız (çünkü $1^2=1$). $-1$ periyodik değildir ama sonunda sabit bir noktaya kilitlenir.

3. Kararlılık Analizi: Çekenler ve İtenler

Bir sabit noktayı bulmak yetmez; onun karakterini de anlamalıyız. Eğer o noktanın biraz yakınından başlarsanız ne olur? Noktaya doğru mu çekilirsiniz (Kararlı), yoksa ondan uzaklaşır mısınız (Kararsız)?

Bunu anlamak için türev ($f’$ ) kullanılır:

• Kararlı: Eğer sabit noktada $\lvert f’(x) \rvert < 1$ ise, o nokta bir bataklık gibidir; yakındaki noktalar ona çekilir.
• Kararsız: Eğer sabit noktada $\lvert f’(x) \rvert > 1$ ise, o nokta bir dağ zirvesi gibidir; yakındaki noktalar oradan itilir.

Manifold Kavramı: Bir sabit noktaya zamanla yakınsayan tüm başlangıç koşullarının oluşturduğu kümeye Kararlı Manifold denir. Örneğin $x^3$ fonksiyonunda $(-1, 1)$ aralığındaki her sayı, küpü alındıkça küçülür ve sonunda 0’a gider. Dolayısıyla $(-1, 1)$ aralığı, 0 noktasının kararlı manifoldudur.

Tersi alınabilen sistemlerde, geçmişe doğru gidildiğinde sabit noktaya ulaşan kümeye de Kararsız Manifold denir.

4. Çember Haritaları: Açılarla Oynamak

Sayı doğrusundan çıkıp bir çember üzerine ($S^1$) geçtiğimizde işler daha ilginçleşir. Burada açılarla ($\theta$) çalışırız ve her şey $2\pi$ modunda döner.

Açı İkiye Katlama

$f(\theta) = 2\theta$ fonksiyonu, çemberdeki açıyı ikiye katlar. Bu, yukarıda bahsettiğimiz “esnetme ve katlama” (hamur) işleminin matematiksel karşılığıdır ve kaos teorisinde çok önemlidir.

Sinüs Haritası Örneği ve Analizi

Şimdi biraz daha karmaşık bir örneğe, sinüs içeren bir çember haritasına bakalım:

Burada $\epsilon$, 0 ile 0.5 arasında küçük bir parametredir.

1. Sabit Noktalar: $\sin(2\theta) = 0$ olan yerlerdir: $0, \pi/2, \pi, 3\pi/2$.
2. Kararlılık Testi: Türev alalım: $f’(\theta) = 1 + 2\epsilon \cos(2\theta)$.
   • $\pi/2$ ve $3\pi/2$ noktalarında: $\cos(2\theta) = -1$ olduğundan türev $1 - 2\epsilon$ olur. $\epsilon$ pozitif olduğu için bu değer 1’den küçüktür. Yani bu noktalar kararlıdır, yakındaki açıları kendilerine çekerler.
   • $0$ ve $\pi$ noktalarında: $\cos(2\theta) = 1$ olduğundan türev $1 + 2\epsilon$ olur. Bu değer 1’den büyüktür. Yani bu noktalar kararsızdır, noktaları iterler.

Bunu görselleştirmek isterseniz, çember üzerinde 0 ve $\pi$ noktalarından çıkan okların $\pi/2$ ve $3\pi/2$ noktalarına doğru aktığını hayal edebilirsiniz.

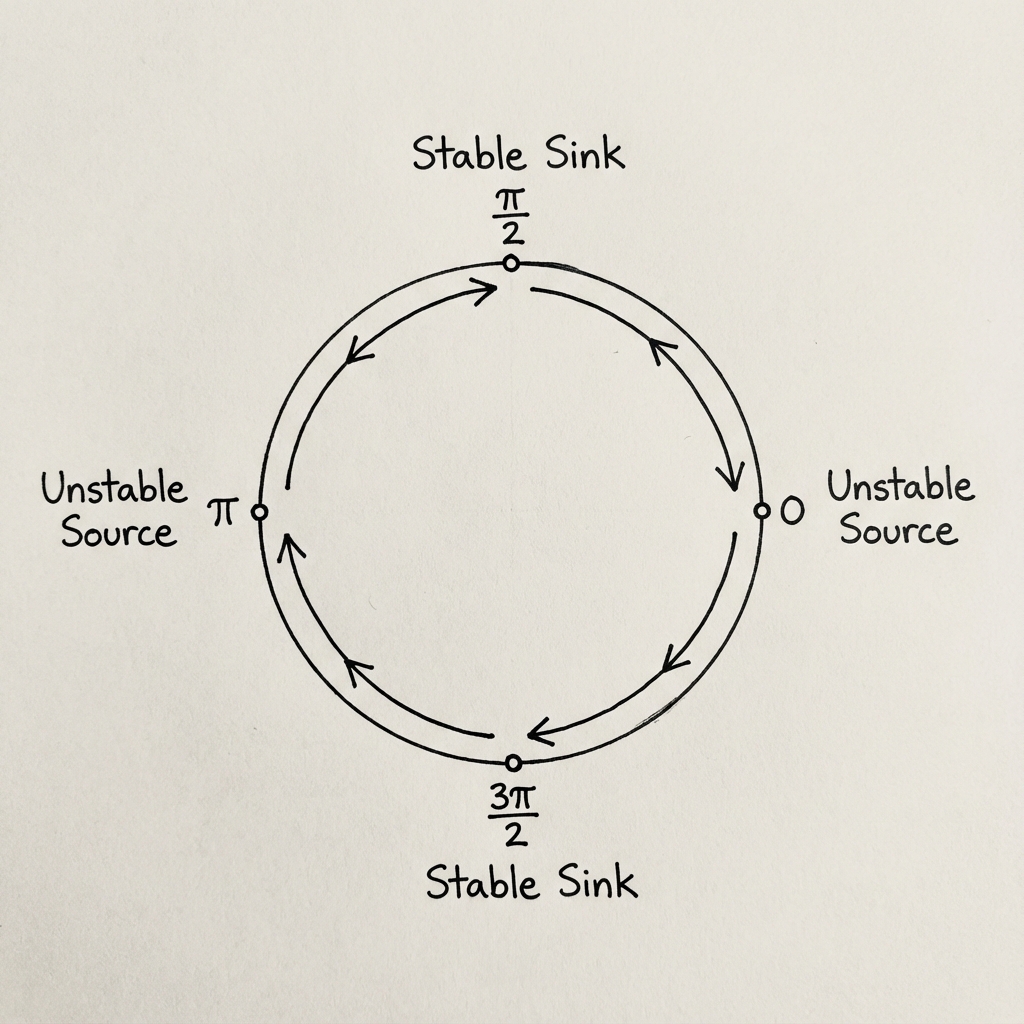Çember haritasındaki vektör alanı: 0 ve $\pi$ noktaları kararsız (kaynak) davranırken, oklar $\pi/2$ ve $3\pi/2$ kararlı noktalarına (kuyu) doğru akmaktadır.

5. Sonuç ve Bir Ödev

Bu yazıda gördüğümüz gibi, sadece $x^3$ veya $x^2-1$ gibi lise matematiğinden tanıdığımız basit fonksiyonlar bile, tekrar edildiklerinde (iterasyon) zengin bir dinamik yapı ortaya çıkarır. Sabit noktalar, periyodik döngüler ve kararlı/kararsız manifoldlar, kaos teorisinin alfabesidir.

Kendin Dene: Bilgisayarın başına geçip $f(\theta) = \theta + \epsilon \sin(n\theta)$ fonksiyonunu kodlamayı deneyin. $n=2$ örneğini yaptık, peki $n=3$ veya daha büyük değerler için sabit noktalar ve kararlılık nasıl değişiyor? $\epsilon$ değeri $1/n$’den büyük olursa ne olur?

Bir sonraki yazıda, bu yapıların “hiperbolisite” kavramıyla nasıl daha kesin bir dille tanımlandığını inceleyebiliriz, ama şimdilik bu “döngüsel” dünyada biraz pratik yapmak en iyisidir.