Otomata Teorisi Sohbetleri: Bölüm 1 - İşin Matematiği

Bilgisayar bilimlerine dışarıdan bakınca olay sadece kod yazmak, arayüz tasarlamak ya da veritabanı yönetmekmiş gibi duruyor. Ama işin aslı pek öyle değil. Bu işin mutfağına, o kodların çalıştığı zemine indiğimizde karşımıza beton gibi sağlam bir yapı çıkıyor: Otomata Teorisi. İnşaat mühendisi için statik neyse, bizim için de otomata o. Bilgisayar bilimlerinin “fizik kuralları” desek yeridir.

Temel derdimiz şu: Elimizdeki makine, bu ister basit bir kahve otomatı olsun, ister süper bilgisayar, mantıksal olarak neleri yapabilir, neleri yapamaz? Bunu anlamak için işlemcilerden, RAM’lerden, kablolardan sıyrılıp tamamen kağıt üzerinde, soyut düşünmemiz gerekiyor. Bir derleyicinin yazdığınız if-else bloğunu nasıl hatasız anladığını, karmaşık metinlerin içinde aradığınız deseni bulan o düzenli ifadelerin nasıl çalıştığını merak ediyorsanız, yolun sonu hep buraya çıkıyor.

Bu yazıda, Shyamalendu Kandar’ın kitabındaki temel kavramlardan yola çıkarak, ileride sıkça karşımıza çıkacak DFA, NFA, Turing Makinesi gibi yapıların temelini atacağız. Ezber boğulmak yok, amacımız şu matematiksel dilin mantığını sökmek.

1. Alfabe, Dizgi ve Diller

Otomata teorisinde her şey, tıpkı bir dili öğrenmeye başlar gibi, en küçük parçaları tanımlamakla başlıyor. Bunlar başta biraz teorik gelebilir ama ileride kuracağımız koca koca makinelerin tuğlaları aslında bunlar.

1.1. Temel Tanımlar

Bir sistemi modellemeden önce, elimizde hangi malzemelerin olduğunu netleştirmemiz lazım.

• Sembol: Bizim atomumuz. Daha küçüğü yok. Tek başına duran en temel veri parçası. Harf olur ($a, b$), rakam olur ($0, 1$) veya özel işaretler olur ($#, $$). Bizim için önemli olan sembolün ne olduğu değil, diğerlerinden farklı olması.
• Alfabe ($\Sigma$): Kullanacağımız tüm sembolleri bir torbaya doldurduğunuzu düşünün, işte o küme. Kural şu: Bu küme sonlu olmak zorunda ve boş olamaz. Elinizde üzerinde çalışacak en az bir malzeme olmalı.
  • Örnek: Bilgisayarların ana dili İkili Alfabe: $\Sigma = {0, 1}$. Bu evrende çalışıyorsak ‘2’ rakamını veya ‘a’ harfini kullanamayız; onlar bizim dünyamızda yok.
• Dizgi / Katar: Alfabedeki sembolleri yan yana dizerek oluşturduğumuz diziler. “Kelime” de diyebiliriz bunlara. Anlamlı olması gerekmiyor; alfabedeki elemanları sıraya dizmek yeterli. Genelde $w, u, v$ gibi harflerle gösteriyoruz.
  • Örnek: $\Sigma = {0, 1}$ ise, $w = 1001$ geçerli bir dizgi.
• Uzunluk ($\lvert w \rvert$): Dizgide kaç tane sembol var? Sayıyoruz, hepsi bu.
  • $w = 001$ ise $\lvert w \rvert = 3$.
• Boş Dizgi ($\lambda$ veya $\epsilon$): İşte burası genelde kafa karıştırır ama çok kritik. İçinde hiç sembol olmayan, uzunluğu 0 olan dizgi. Matematikteki 0 sayısı veya boş küme neyse, burada da $\epsilon$ o. “Hiçbir şey yazmamak” da teknik olarak bir durumdur ve birçok algoritma ya buradan başlar ya da burada biter. Unutmayın, $\lvert \epsilon \rvert = 0$.

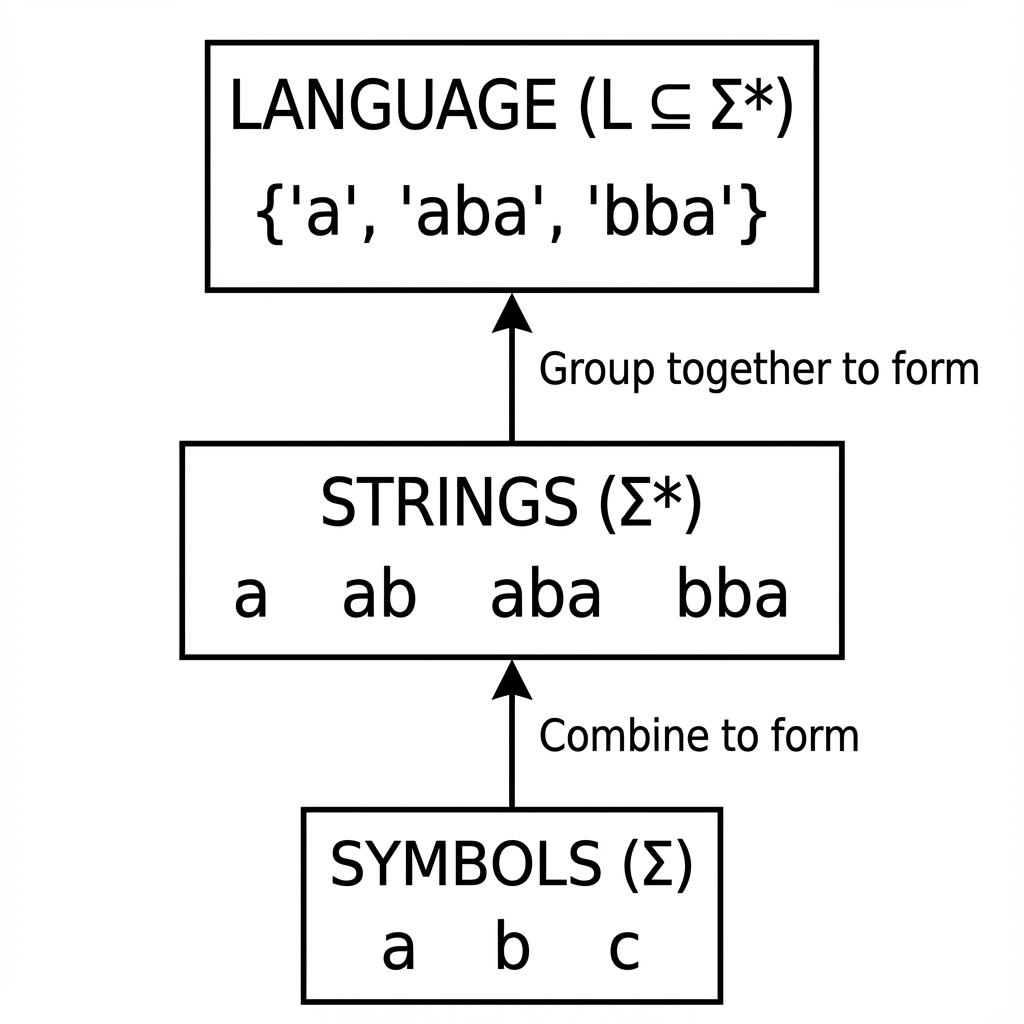Şekil 1: Otomata teorisinin hiyerarşisi. En altta yapı taşımız olan Semboller (a, b) bulunur. Bunlar birleşerek Dizgileri (aba), dizgiler de bir araya gelerek Dilleri oluşturur.

1.2. Dizgilerle Oynamak (String Operasyonları)

Sayılarla nasıl dört işlem yapıyorsak, dizgilerle de bazı işlemler yapabiliyoruz. Makinelerin kelimeleri nasıl işlediğini modellemek için bunlara mecburuz.

• Birleşme: İki dizgiyi alıp, araya boşluk falan koymadan uç uca eklemek. $x$ ve $y$ diye iki dizginiz varsa, yapıştırınca $xy$ oluyor.
  • Örnek: $x = kara$, $y = kedi$ ise, $xy = karakedi$ olur. $yx = kedikara$ olur, yani sıra önemli.
  • Ufak bir detay: Boş dizgi ($\epsilon$) burada etkisiz elemandır. Bir kelimenin yanına “hiçbir şey” eklerseniz, kelime değişmez: $w \epsilon = \epsilon w = w$.
• Kuvvet Alma (Üs Alma): Bir dizgiyi kendisiyle tekrar tekrar birleştirmek.
  • $w^0 = \epsilon$: Bir şeyin sıfırıncı kuvveti matematikte nasıl 1 ise, burada da boş dizgidir. Hiçliktir.
  • $w^1 = w$: Kendisi.
  • $w^2 = ww$: Kendisiyle bir kere birleşimi.
  • Örnek: $w = ab$ ise $w^3 = ababab$. Döngüleri modellemek için birebir.
• Önek ve Sonek: Bir dizgiyi analiz ederken bazen başını sonunu ayırmamız gerekir.
  • $w$ dizgisi $x$ ve $y$ parçalarından oluşuyorsa ($w = xy$):
    • $x$, bu dizginin önekidir (başı).
    • $y$, bu dizginin sonekidir (sonu).
  • Örnek: $w = ban$ kelimesi için:
    • Önekler: $\epsilon, b, ba, ban$.
    • Sonekler: $\epsilon, n, an, ban$.
  • Dikkat ettiyseniz boş dizgi ($\epsilon$) ve kelimenin kendisi hem başta hem sonda var. “Has Önek” dediğimizde kelimenin tamamını hariç tutuyoruz.

2. Kümeler ve Biçimsel Diller

Otomata teorisinde “Dil” dediğimizde aklınıza Türkçe, İngilizce gibi gramer kuralları olan karmaşık yapılar gelmesin. Bizim için dilin tanımı çok net ve sade: Belli bir alfabe ile oluşturulabilecek tüm olası dizgilerin içinden seçilmiş herhangi bir alt küme.

Bu küme sonlu da olabilir (mesela sadece “evet” ve “hayır” kelimeleri), sonsuz da olabilir (tüm asal sayılar gibi). Dil teknik olarak bir küme olduğu için, kümelerle yaptığımız her şeyi (birleşim, kesişim, fark) burada da yapabiliyoruz. Ama otomata teorisine has iki özel işlemimiz daha var.

2.1. Diller Üzerindeki Özel İşlemler

Diyelim ki $A$ ve $B$ diye iki dilimiz (kümemiz) var.

2.1.1. Dillerin Birleşimi

Bu işlem, birinci kümeden bir kelime seçip, ikinci kümeden bir kelimeyle birleştirmektir. Kartezyen çarpım gibi düşünün ama ikililer değil, birleşik kelimeler oluşuyor.

• Örnek: $A = {iyi, kötü}$ ve $B = {kedi, köpek}$ olsun.
• $A \cdot B$ kümesi şunları içerir: ${iyikedi, iyiköpek, kötükedi, kötüköpek}$.

Dillerin yapısını oluştururken kelimelerin nasıl yan yana geleceğini böyle modelliyoruz.

2.1.2. Kleene Yıldızı ($\Sigma^*$)

Otomata teorisinin en meşhur, en “yıldız” operatörü budur. Bir alfabeden veya kümeden üretilebilecek, akla gelebilecek her türlü sonlu dizgiyi kapsayan devasa (sonsuz) kümeyi ifade eder.

Formül karışık durabilir ama mantığı basit:

• $\Sigma^0 = { \epsilon }$ (Hiçbir harf seçmemek, yani boşluk).
• $\Sigma^1 = \Sigma$ (Tek harfliler).
• $\Sigma^2$ (İki harfli tüm kombinasyonlar).
• Ve bu böyle sonsuza kadar gider…

Önemli Not: $\Sigma^*$ kümesi sonsuzdur ama içindeki her bir kelime mutlaka sonlu uzunluktadır. Sonsuz uzunlukta bir kelime bu kümede yer almaz. Bu ayrım teorik tutarlılık için çok kritik.

Bir de Pozitif Kapanış ($\Sigma^+$) var. Bu da Kleene Yıldızı’nın aynısı, tek farkı içinde boş dizgi ($\epsilon$) yok. Yani “en az bir harf olsun” dediğimiz durumlar için kullanıyoruz.

3. Bağıntılar ve Denklik

Makineleri tasarlarken farklı durumların birbirleriyle ilişkisini anlamamız gerekiyor. Bazen iki farklı durum, dışarıdan bakıldığında aslında aynı işi yapıyor olabilir. Bu durumda onları “denk” kabul edip birleştirebiliriz. İşte bu “denklik” kavramının matematiksel karşılığı Bağıntılardır.

Bir $R$ bağıntısının “Denklik Bağıntısı” olabilmesi için şu üç şartı sağlaması gerekir (Bunlar aslında eşitliğin temel özellikleridir):

1. Yansıma: Her eleman kendisiyle bağıntılıdır. $a$, $a$ ile denktir. Aynaya bakmak gibi.
2. Simetrik: İlişki karşılıklıdır. $a$, $b$ ile denkse; $b$ de $a$ ile denk olmalıdır. Tek taraflı eşitlik olmaz.
3. Geçişli: İlişki zincirleme devam eder. $a$, $b$ ile; $b$ de $c$ ile denkse; o zaman $a$ ve $c$ de birbirine denktir.

Neden Bu Kadar Önemli? İleride “Myhill-Nerode Teoremi” gibi konulara geldiğimizde, bir dili tanıyan en küçük makineyi bulmaya çalışacağız. Orada, birbirine “denk” olan durumları tespit edip “bunları tek bir durum yapalım” diyeceğiz. İşte o işlemin matematiksel dayanağı burası.

Pratik Bir Örnek: Tam sayılar kümesi üzerinde şöyle bir kural koyalım: İki sayının farkı ($a - b$) 3’e tam bölünüyorsa, bu sayılar bağıntılıdır ($a \equiv b \pmod 3$). Bakalım bu bir denklik bağıntısı mı?

• Kontrol Edelim:
  • Yansıma: $a - a = 0$. Sıfır, 3’e bölünür mü? Evet.
  • Simetrik: $a - b$ 3’ün katıysa, $b - a$ da 3’ün katıdır (sadece işareti değişir). Evet.
  • Geçişli: $(a - b)$ ve $(b - c)$ 3’ün katıysa, bunları topladığımızda $b$’ler gider ve $(a - c)$ kalır. İki tane 3’ün katı olan sayının toplamı yine 3’ün katıdır. Evet.

Demek ki bu bir denklik bağıntısı. Bu bağıntı tüm tam sayıları 3 gruba ayırır: 3’e tam bölünenler, 1 kalanını verenler ve 2 kalanını verenler. Otomata teorisinde de durumları aynen bu mantıkla gruplayacağız.

4. İspat Yöntemi: Tümevarım

Otomata teorisinde sıkça karşımıza çıkan bir sorun var: “Tasarladığım bu makine, sonsuz sayıdaki tüm olası girdiler için doğru çalışıyor mu?” Bunu tek tek deneyerek kanıtlayamayız, ömür yetmez. Bu noktada matematiğin en güçlü silahlarından biri olan Tümevarım devreye giriyor.

Mantık şu:

1. Temel Adım: İddianın en küçük, en basit durum için (genellikle boş dizgi için) doğru olduğunu gösteriyoruz.
2. Varsayım: İddianın, belli bir $n$ uzunluğuna kadar olan tüm dizgiler için doğru olduğunu varsayıyoruz.
3. Kanıt: Bu varsayımı kullanarak, iddianın $n+1$ uzunluğundaki dizgiler için de mecburen doğru olması gerektiğini kanıtlıyoruz.

Dominoları dizmek gibi düşünün; ilki devrilirse ve her taş bir sonrakini devirecek şekilde dizilmişse, hepsi devrilir. Bu yöntem, dillerin özelliklerini veya gramerlerin doğruluğunu ispatlarken elimiz ayağımız olacak.

5. Graf Teorisi ve Otomatlar

Tahtada veya kitaplarda gördüğünüz o yuvarlaklar ve oklar çizimi, aslında rastgele şekiller değil; matematiksel birer Graftır. Daha doğrusu, Sonlu Otomatlar birer “Yönlü Graf”tır.

Bir otomatayı matematiksel olarak tanımlarken şu iki kavramı kullanıyoruz:

• Köşeler: Grafın noktaları. Biz bunlara Otomata dünyasında Durumlar diyoruz. Makinenin o anki hafızasını veya pozisyonunu temsil ediyorlar.
• Kenarlar: Köşeleri birbirine bağlayan oklar. Bunlar da Geçişler. Yani “şu sembolü okursam hangi duruma gitmeliyim?” sorusunun cevabı.

Bir de Yol kavramı var. Başlangıç düğümünden çıkıp, okları takip ederek başka bir düğüme gitme işi. Otomata teorisinde bunun karşılığı şu: Makine başlangıç durumundan ($q_0$) çalışmaya başlar, girdiğimiz kelimenin harflerini takip ederek bir yol izler. Eğer bu yolun sonu bir “Kabul Durumu”na çıkıyorsa, işlem tamamdır, makine o kelimeyi kabul etmiştir.

Son olarak Ağaç yapısını unutmayalım. Döngüsü olmayan, dallanıp budaklanan bu graf türünü, ileride bir cümlenin gramer yapısını analiz ederken “Ayrıştırma Ağacı” olarak bol bol kullanacağız.

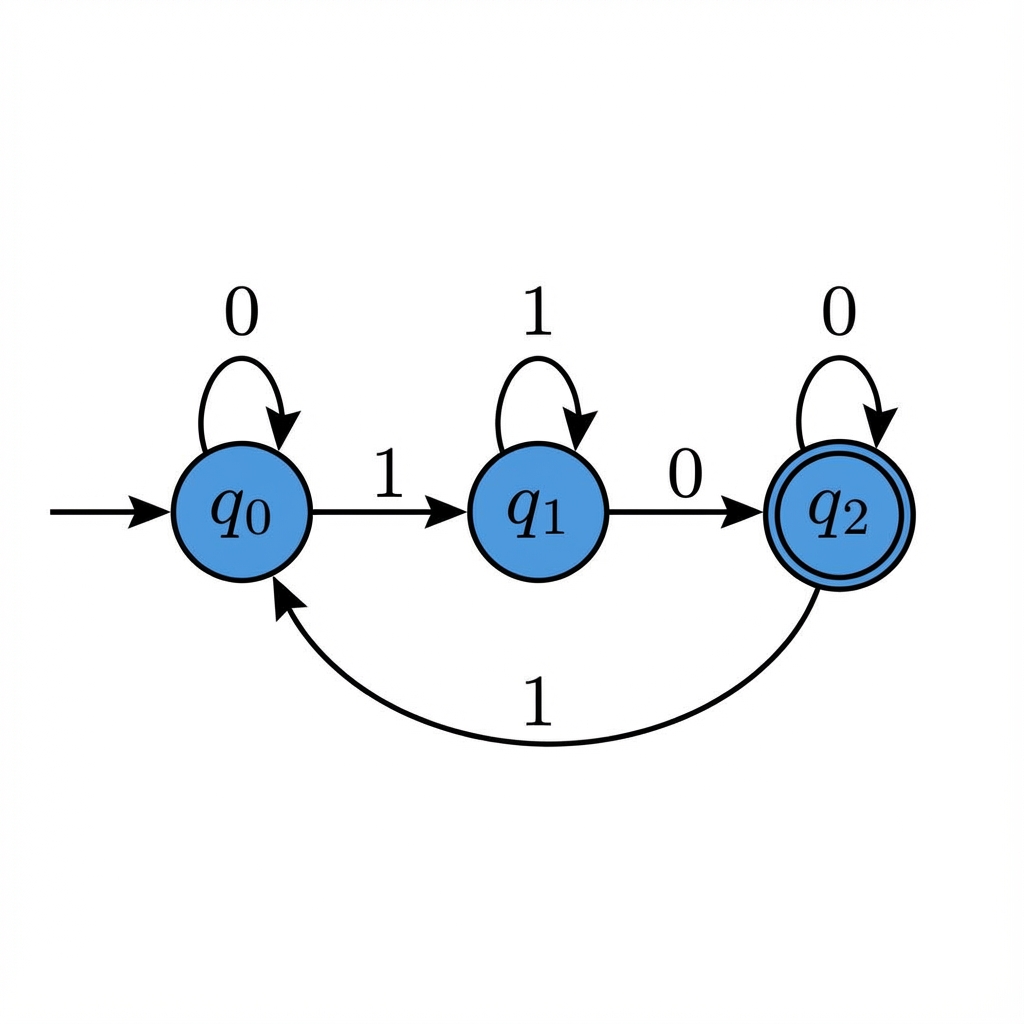Şekil 2: Basit bir Deterministik Sonlu Otomat (DFA). $q_0$ başlangıç durumudur. Oklar (geçişler), gelen sembole göre (0 veya 1) hangi duruma gidileceğini gösterir. Çift daire ile gösterilen $q_2$ ise kabul durumudur.

Görselin Derinlemesine Analizi: Bu Makine Nasıl Çalışır?

Şekil 2’deki diyagram, soyut bir makinenin “beyninin” haritasıdır. Bu çizimi sadece yuvarlaklar ve oklar olarak değil, bir yol haritası olarak görmelisiniz. İşte adım adım çalışma mantığı:

1. Başlangıç Noktası ($q_0$):
   • Her yolculuk buradan başlar. Diyagramda $q_0$’a dışarıdan gelen (bir yerden çıkmayan) o küçük ok, “Start” yani başlangıç noktasını gösterir.
   • Makine ilk açıldığında hafızası $q_0$ durumundadır.
2. Karar Anları (Geçişler/Oklar):
   • Okların üzerindeki 0 ve 1 rakamları, makineye gelen girdilerdir (input).
   • Makine o an hangi durumdaysa (örneğin $q_0$), gelen karaktere bakar ve ilgili oku takip eder.
   • Bu, kodlamadaki if (input == '0') goto q1; mantığının görsel halidir.
3. Hafıza (Durumlar/States):
   • $q_0, q_1, q_2$ yuvarlakları makinenin o anki “modunu” veya hafızasını temsil eder.
   • Makine geçmişte ne okuduğunu hatırlamaz, sadece “şu an neredeyim?” bilgisini tutar. Geçmişin tüm özeti, o an bulunulan durumdur.
4. Hedef (Kabul Durumu - $q_2$):
   • $q_2$’nin etrafındaki çift daire, buranın “mutlu son” olduğunu gösterir.
   • Eğer elimizdeki kelimenin tüm harflerini okuyup bitirdiğimizde, parmağımız bu çift daireli $q_2$ üzerinde duruyorsa, makine bu kelimeyi KABUL ETMİŞTİR.
   • Eğer tek daireli bir yerde ($q_0$ veya $q_1$) durursak, kelime REDDEDİLMİŞTİR.

Özetle: Bu görsel, bir kelimenin “doğru” olup olmadığını kontrol eden bir doğrulama algoritmasının şemasıdır. Parmağınızı $q_0$’a koyun, kelimenizdeki harflere göre okları takip edin. Son durak çift daire ise kazandınız

Toparlarsak

Bu bölümde, karmaşık makineleri ve dilleri analiz etmek için ihtiyacımız olan alet çantasını hazırladık. Sembollerin nasıl birleşip dizgileri, dizgilerin nasıl birleşip dilleri oluşturduğunu gördük. Sonsuzluğu ifade etmek için Kleene Yıldızı’nı, durumları gruplamak için denklik bağıntılarını ve makineleri çizmek için graf teorisini tanıdık.

Artık elimizde sağlam bir zemin var. Bir sonraki bölümde, bu kavramları kullanarak Biçimsel Diller ve Gramerler konusuna gireceğiz. Dilleri karmaşıklıklarına göre sınıflandıran o meşhur “Chomsky Hiyerarşisi”ni inceleyip, Düzenli Dillerden başlayarak yukarı doğru tırmanacağız.

Sıra Sizde

Konuyu pekiştirmek için şu soruya bir bakın: $S = {0, 1}$ alfabesiyle oluşturulabilecek, uzunluğu en fazla 2 olan tüm dizgilerin kümesini yazabilir misiniz? (Ufak bir ipucu: Hiçbir şey yazmamak da bir seçenektir, $\epsilon$’u unutmayın!)

(Cevap: ${\epsilon, 0, 1, 00, 01, 10, 11}$)