Graf Teorisi: Noktalar, Çizgiler ve Bağlantıların Matematiği

Günlük hayatta metro haritalarından sosyal ağlara, elektrik devrelerinden internetin yapısına ve hatta moleküler kimyaya kadar her yerde karşımıza çıkan karmaşık ağları hiç düşündünüz mü? Görünüşte birbirinden tamamen farklı olan bu sistemlerin ortak bir dili vardır. Matematikçiler bu yapıları ve aralarındaki ilişkileri incelemek için Graf Teorisi (Graph Theory) adını verdikleri zarif, güçlü ve son derece görsel bir dil kullanırlar.

Bu yazıda, J.A. Bondy ve U.S.R. Murty’nin bu alandaki temel eseri olan “Graph Theory with Applications” kitabından yola çıkarak, graf teorisinin temellerine, en büyüleyici teoremlerine ve matematiksel denklemlerine derinlemesine bir yolculuk yapacağız. Sadece formüllere değil, bu formüllerin ne anlama geldiğine de yakından bakacağız.

1. Graf Nedir? Temel Tanımlar

En basit haliyle bir graf, noktalar (köşeler) ve bu noktaları birleştiren çizgilerden (kenarlar) oluşur. Ancak graf teorisinde önemli olan bu çizimin nasıl göründüğü değil, hangi noktanın hangi noktaya bağlı olduğudur. Matematiksel olarak bir $G$ grafı, boş olmayan bir $V(G)$ köşe kümesi ve bu köşeler arasındaki ilişkileri tanımlayan $E(G)$ kenar kümesi ile ifade edilir:

Burada kullanılan temel parametreler şunlardır:

• $\nu(G) = \lvert V \rvert$: Grafın köşe sayısı (order). Örneğin bir sınıftaki öğrenci sayısı.
• $\epsilon(G) = \lvert E \rvert$: Grafın kenar sayısı (size). Örneğin bu öğrenciler arasındaki toplam arkadaşlık bağı sayısı.

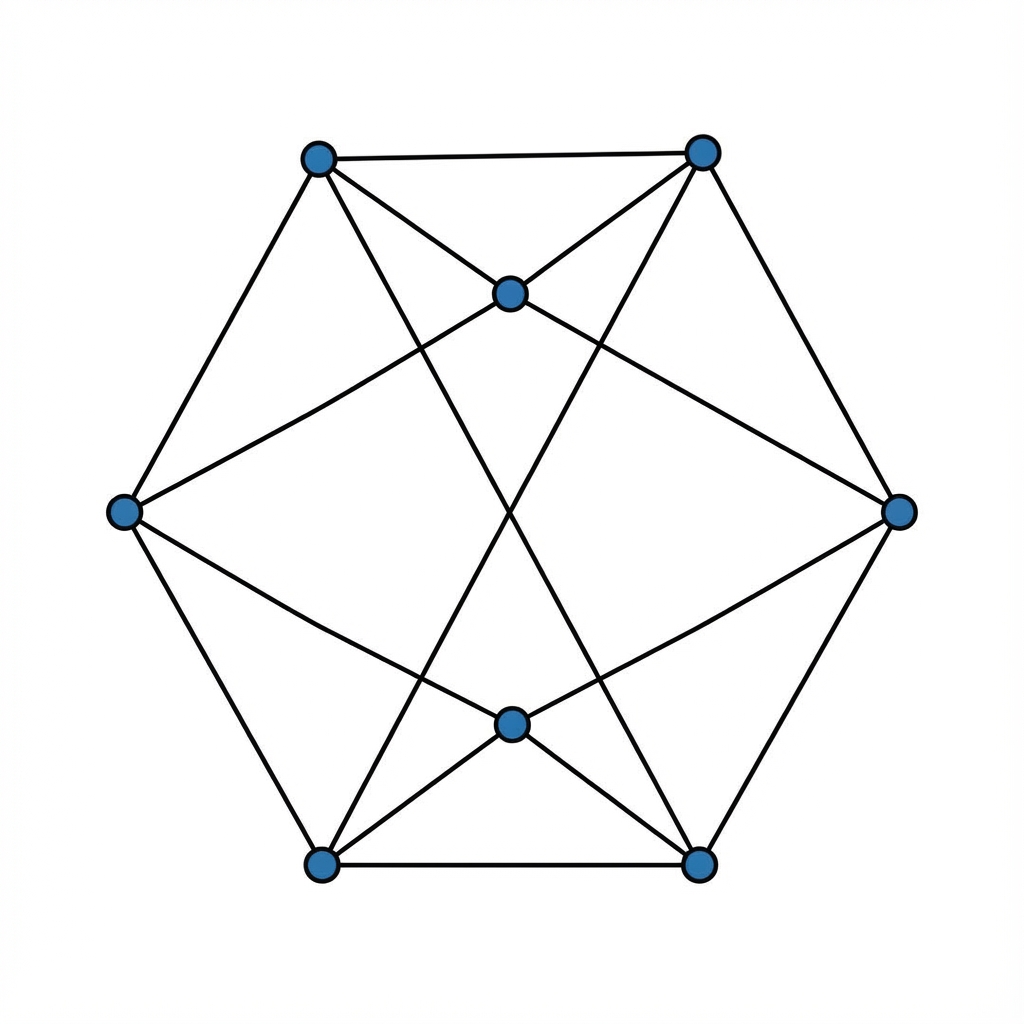
Örneğin, bir arkadaşlık ağında köşeler insanları, kenarlar ise arkadaşlık bağlarını temsil eder. Eğer kenarların yönü varsa (örneğin Twitter’da birini takip etmek gibi, bu ilişki karşılıklı olmak zorunda değilse), buna Yönlü Graf (Digraph) denir. Yönlü graflar, tek yönlü yolların olduğu şehir trafiğini veya bir web sayfasından diğerine verilen linkleri modellemek için mükemmeldir.

2. Tokalaşma Lemması (The Handshaking Lemma)

Graf teorisindeki ilk ve en temel teoremlerden biri, köşelerin dereceleri ile kenar sayısı arasındaki ilişkiyi açıklar. Bir $v$ köşesinin derecesi $d(v)$, o köşeye bağlı olan kenar sayısıdır; yani o noktanın “komşu” sayısıdır.

Mantıken düşünelim: Her kenar iki uca sahiptir, yani tam olarak iki köşeyi birbirine bağlar. Bir kenarı saydığımızda, aslında iki farklı köşenin derecesine +1 katkıda bulunmuş oluruz. Dolayısıyla, bir graftaki tüm dereceleri toplarsak, kenar sayısının tam olarak iki katını elde ederiz. Bondy ve Murty’nin kitabında Teorem 1.1 olarak geçen ve graf teorisinin “ilk kanunu” sayılabilecek eşitlik şöyledir:

Bu basit denklemden, sosyal ortamlarda sıkça anlatılan şu şaşırtıcı ama kesin sonuç çıkar: Herhangi bir grafta (veya bir partide), derecesi tek sayı olan köşelerin (tek sayıda el sıkışmış kişilerin) sayısı daima çifttir. Tek sayıda el sıkışan tek sayıda insan olması matematiksel olarak imkansızdır.

3. Matrislerle Gösterim: Komşuluk ve İnsidens

Grafları kağıt üzerine çizmek insanlar için harikadır, ancak bu yapıları bilgisayarlara anlatmanın en iyi yolu matrislerdir.

Komşuluk Matrisi (Adjacency Matrix)

Bir $G$ grafının köşeleri $v_1, v_2, …, v_n$ olsun. $n \times n$ boyutundaki $A(G) = [a_{ij}]$ matrisi, ağın dijital bir haritası gibidir ve şöyle tanımlanır:

• Eğer $v_i$ ve $v_j$ arasında bir kenar varsa $a_{ij} = 1$ (veya o iki nokta arasındaki bağlantı sayısı).
• Yoksa $a_{ij} = 0$.

Matematiksel olarak bu matrisin kuvvetleri bize graftaki yollar (walks) hakkında derin bilgiler verir. Örneğin, $A^2$ matrisini hesapladığınızda, $(i, j)$ hücresindeki sayı, $i$ ve $j$ kişilerinin “ortak arkadaş sayısını” verir. Daha genel olarak, $A^k$ matrisinin $(i, j)$ elemanı, $v_i$ ile $v_j$ arasında uzunluğu $k$ olan farklı yolların sayısını verir. Bu özellik, “bu iki nokta birbirine ne kadar yakın?” veya “kaç farklı yoldan ulaşabilirim?” sorularını yanıtlayan algoritmaların temelidir.

4. Ağaçlar (Trees) ve Ormanlar

Döngü içermeyen (acyclic) ve bağlantılı graflara Ağaç denir. Eğer bir yapı bağlantılı değilse ama döngü içermiyorsa, birden fazla ağacın birleşimi olduğu için buna Orman (Forest) denir. Ağaçlar, soy ağaçlarından bilgisayar dosya sistemlerine, html yapısından karar verme algoritmalarına kadar hiyerarşik verilerin modellenmesinde hayati öneme sahiptir.

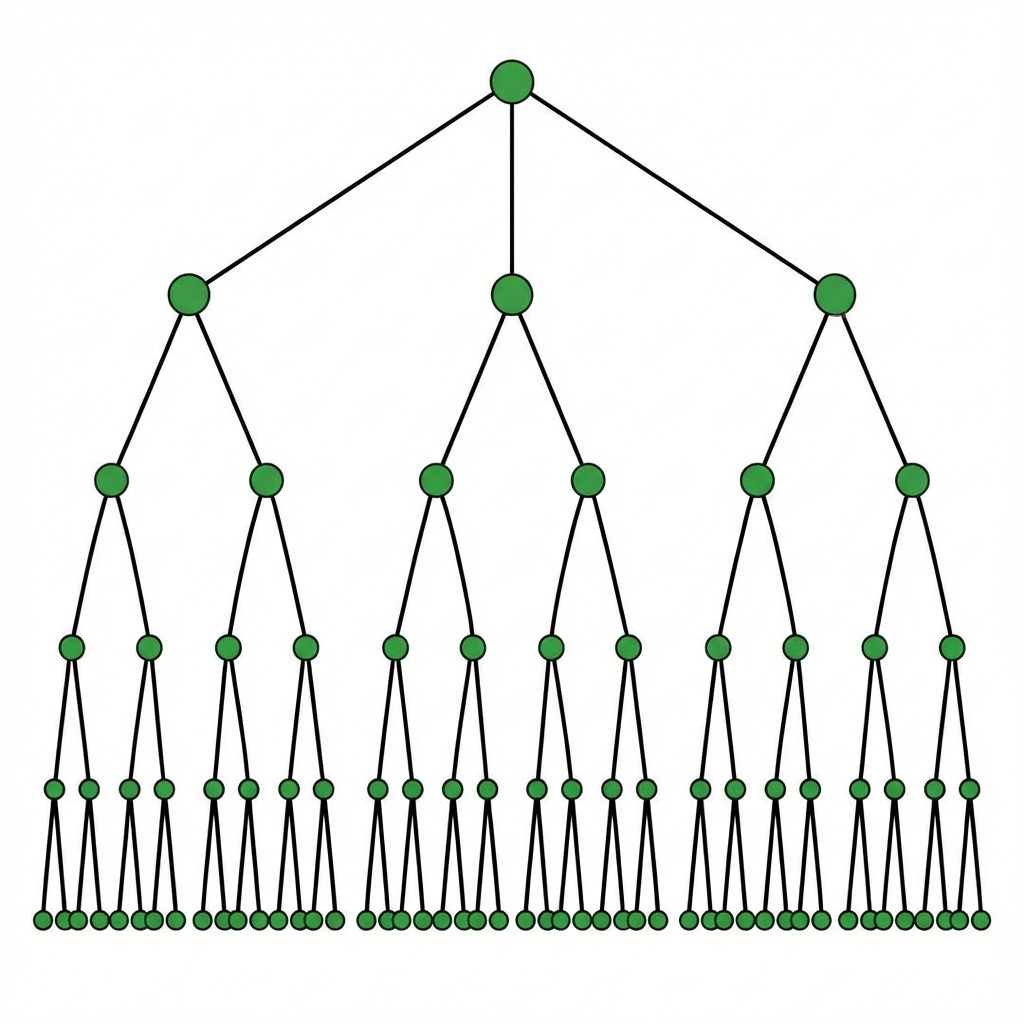
Bir ağacın en belirgin özelliği, en az sayıda kenar ile tüm noktaları birbirine bağlamasıdır. Bir ağacın kenar sayısı ile köşe sayısı arasında her zaman sabit ve basit bir ilişki vardır (Teorem 2.2):

Yani $n$ köşeli bir ağacın her zaman, istisnasız $n-1$ kenarı vardır. Bir kenar daha eklerseniz mutlaka bir döngü oluşur; bir kenar çıkarırsanız ağaç parçalanır ve bağlantı kopar.

Cayley Formülü

Peki, $n$ tane etiketli (birbirinden ayırt edilebilir) köşe ile kaç farklı ağaç oluşturulabilir? Bu sorunun cevabı meşhur Cayley Formülü ile verilir. $K_n$ (n köşeli tam graf) içindeki tüm köşeleri kapsayan ağaç (spanning tree) sayısı $\tau(K_n)$ şu muazzam denklemle bulunur:

Örneğin sadece 4 köşe ile ($4^{4-2}$) tam 16 farklı ağaç yapısı kurabilirsiniz. Sayı arttıkça, olasılıkların ne kadar hızlı büyüdüğünü hayal edin; bu da ağ yapıların ne kadar zengin olabileceğini gösterir.

5. Düzlemsel Graflar ve Euler Formülü

Bir grafı, kenarları birbirini kesmeyecek şekilde (köprüler veya tüneller kullanmadan) bir kağıda çizebiliyorsak, bu grafa Düzlemsel Graf (Planar Graph) denir.

Her graf düzlemsel değildir. Graf teorisinin en ünlü problemlerinden biri olan “Üç Ev ve Üç Kuyu” problemi, $K_{3,3}$ grafının (3 evin her birinin 3 kuyuya da bağlanması) düzlem üzerine kenarlar kesişmeden çizilemeyeceğini gösterir. Aynı durum 5 noktanın her birinin diğerine bağlandığı $K_5$ için de geçerlidir. Bu iki graf, düzlemselliğin önündeki temel engellerdir.

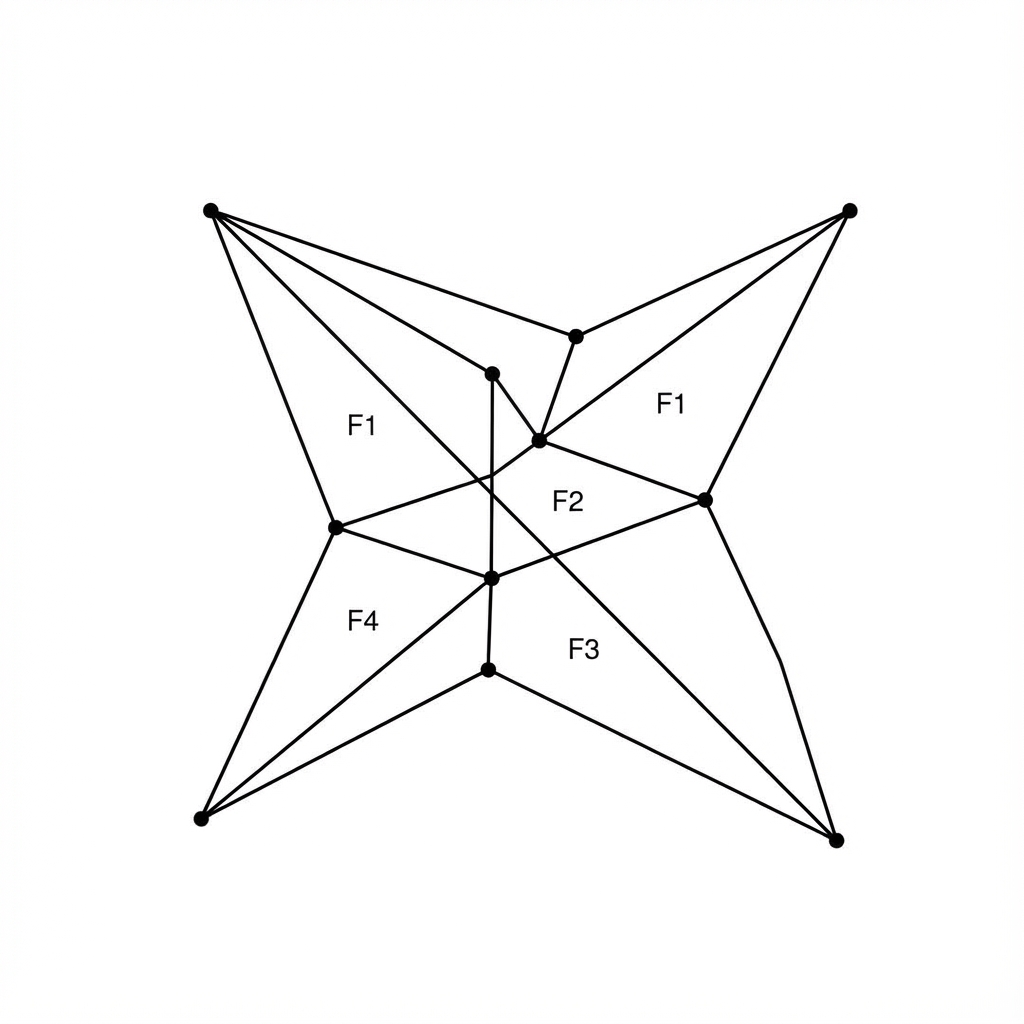
Düzlemsel graflar çizildiğinde, düzlemi “yüz” adı verilen bölgelere ayırır (buna grafın dışındaki sonsuz alan da dahildir). Leonhard Euler, bağlantılı düzlemsel graflar için köşe ($\nu$), kenar ($\epsilon$) ve yüz ($\phi$) sayıları arasında sarsılmaz bir ilişki bulmuştur (Teorem 9.5):

Bu formül, sadece graflar için değil, 3 boyutlu çokyüzlüler (polyhedra) geometrisinin de temelidir. Örneğin bir küp düşünelim:

• Köşe ($\nu$) = 8
• Kenar ($\epsilon$) = 12
• Yüz ($\phi$) = 6 (Küpün kare yüzeyleri)

Denklem: $8 - 12 + 6 = 2$. Matematik, şekil ne olursa olsun değişmez!

6. Graf Renklendirme

Harita boyama problemlerinden doğan bu alan, bir grafın köşelerini, birbirine komşu olan herhangi iki köşe aynı renkte olmayacak şekilde boyamayı hedefler. Bir grafı boyamak için gereken minimum renk sayısına Kromatik Sayı denir ve $\chi(G)$ ile gösterilir.

Bu konu sadece haritaları boyamakla ilgili değildir; ders programı hazırlama (scheduling) problemleri de aslında birer graf boyama problemidir. Eğer dersleri köşeler, çakışan saatleri kenarlar olarak düşünürseniz, gereken minimum renk sayısı, sınavları yapmak için gereken minimum oturum sayısını verir.

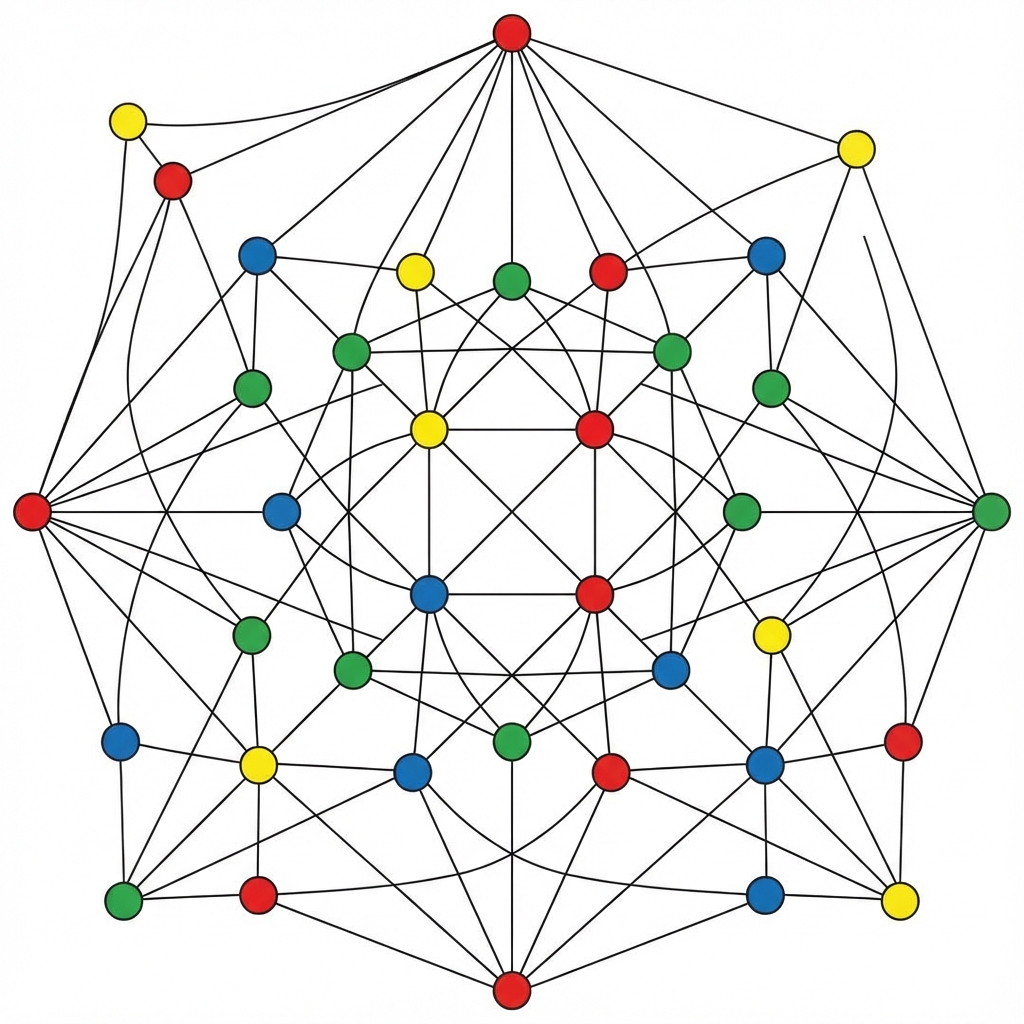
Meşhur Dört Renk Teoremi, herhangi bir düzlemsel grafın (veya haritanın) en fazla 4 renk ile boyanabileceğini söyler. Ancak genel (düzlemsel olmayan) graflar için Brooks Teoremi (Teorem 8.4) şu üst sınırı verir:

Eğer $G$ grafı tek bir döngü veya tam graf ($K_n$) değilse:

Burada $\Delta(G)$, graftaki bir köşenin sahip olduğu maksimum derecedir. Yani en çok arkadaşı olan kişinin arkadaş sayısı, bize ihtiyaç duyacağımız maksimum renk sayısı hakkında bir fikir verir.

Sonuç

Graf teorisi, 1736’da Königsberg’in yedi köprüsünden geçip geçemeyeceğimizi sorgulayan basit bir bulmacadan, bugün modern internetin veri akışını, yapay zeka ağlarını ve lojistik devlerinin rotalarını optimize eden devasa bir bilime dönüşmüştür.

Bondy ve Murty’nin kitabında da gösterildiği gibi, sadece birkaç nokta ve çizgi ile başlayan bu yapı, $\nu - \epsilon + \phi = 2$ gibi evrensel doğrulara ulaşmamızı sağlar. Bir dahaki sefere bir metro haritasına baktığınızda, bir çip tasarımını incelediğinizde veya sosyal medyada “ortak arkadaşlarınızı” gördüğünüzde, arka planda sessizce işleyen bu muazzam matematiksel çarkları hatırlayın.