Geometry
Konveks Geometrinin Kalbi: Carathéodory Teoremi
November 29, 2025
Bazı teoremler vardır, duyduğunuzda “Hah, evet mantıklı” dersiniz. Bazıları da kafanızda dönüp durur, “E bir dakika, durun bakalım, nasıl oluyor bu iş?” dersiniz. Carathéodory Teoremi tam olarak ikinci türden. 1911’de Constantin Carathéodory diye Yunan asıllı bir adam, konveks kümelerle uğraşırken muazzam bir şey fark etti. Ve bu fark edişin üstünden 100 yıl geçmesine rağmen hala kullanıyoruz: makine öğrenmesinde, grafiklerde, optimizasyonda, her yerde.
Bu yazıda size bu teoremin ne anlama geldiğini, neden bu kadar kritik olduğunu ve matematiksel ispatını göstereceğim. Ama önce biraz zemin hazırlayalım.
Konveks Örtü: Lastik Bant Gibi Düşünün
Carathéodory’yi anlamak için önce “konveks örtü” ne demek bilmemiz lazım. Şöyle düşünün: Duvara bir sürü raptiye çakmışsınız. Şimdi elinize kocaman bir lastik bant alıp bütün raptiyelerin etrafını sarıyorsunuz. Bırakıyorsunuz. Lastik kendiliğinden geriliyor, en dıştaki raptiyelere yapışıyor. İşte bu lastiğin çizdiği şekil, o noktaların konveks örtüsü.
Matematikçiler buna şöyle der: Bir $P$ nokta kümesinin konveks örtüsü ($\text{conv}(P)$), bu noktaları belli ağırlıklarda karıştırarak elde edebileceğiniz tüm noktaları içeren en küçük dışbükey kümedir. Ama size bu lastik bant hikayesi daha iyi oturur muhtemelen.
Teorem: Boyut Her Şeyi Belirliyor
Carathéodory’nin dediği şu: $d$ boyutlu uzayda bir konveks örtünün içindeki herhangi bir noktayı bulmak için en fazla $d+1$ nokta yeter. Hepsi bu.
Bir daha söyleyeyim çünkü çok güçlü bir iddia bu: Kaç tane noktanız olursa olsun (bin tane de olsa, milyon tane de olsa), içlerinden herhangi birini ifade etmek için sadece $d+1$ tanesine ihtiyacınız var.
$x \in \text{conv}(P)$ ve $P \subset \mathbb{R}^d$ ise, öyle $p_0, p_1, \ldots, p_d \in P$ noktaları bulabilirsiniz ki:
\[x = \sum_{i=0}^{d} \lambda_i p_i\]Katsayılar:
- $\lambda_i \ge 0$ (negatif değil)
- $\sum_{i=0}^{d} \lambda_i = 1$ (toplamları 1, yani bir ağırlıklı ortalama)
Somut Bakalım
1 boyutta: Bir çizgi düşünün. O çizgi üzerindeki herhangi bir nokta, iki ucunun ağırlıklı ortalamasıdır. Mesela 0 ile 10 arasında 7, şu şekilde: $7 = 0.3 \times 0 + 0.7 \times 10$. Yani 2 nokta ($1+1$) yetti.
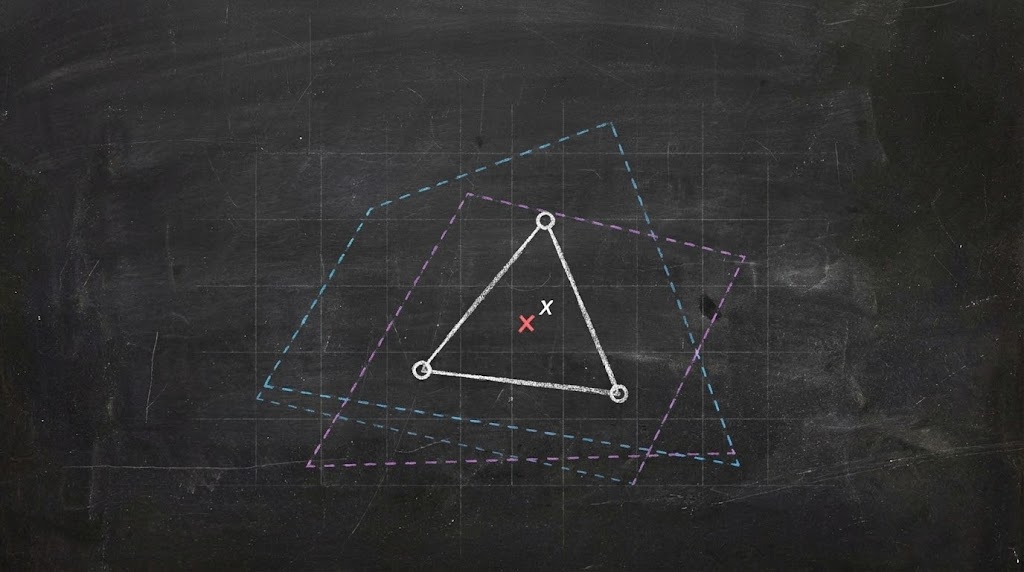
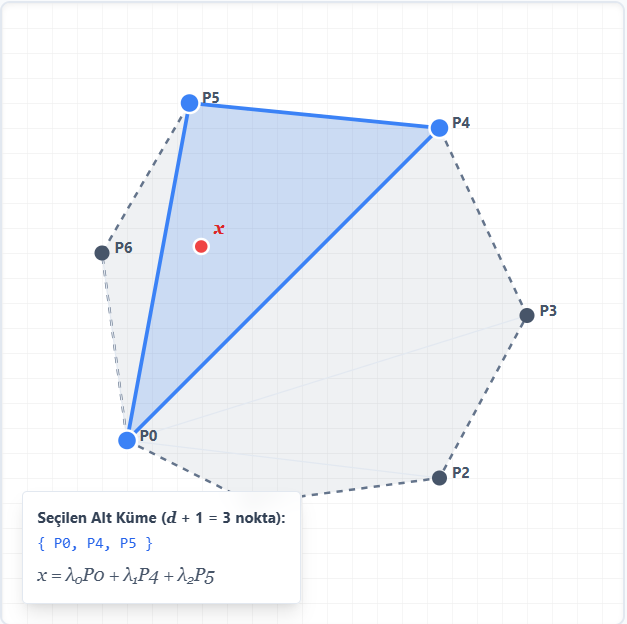
2 boyutta: Bir çokgen içindeki herhangi bir nokta, o çokgenin köşelerinden 3 tanesinin ($2+1$) oluşturduğu bir üçgenin içindedir.
3 boyutta: Bir cismin içindeki herhangi bir nokta, 4 köşenin ($3+1$) oluşturduğu piramidin (tetrahedron) içindedir.
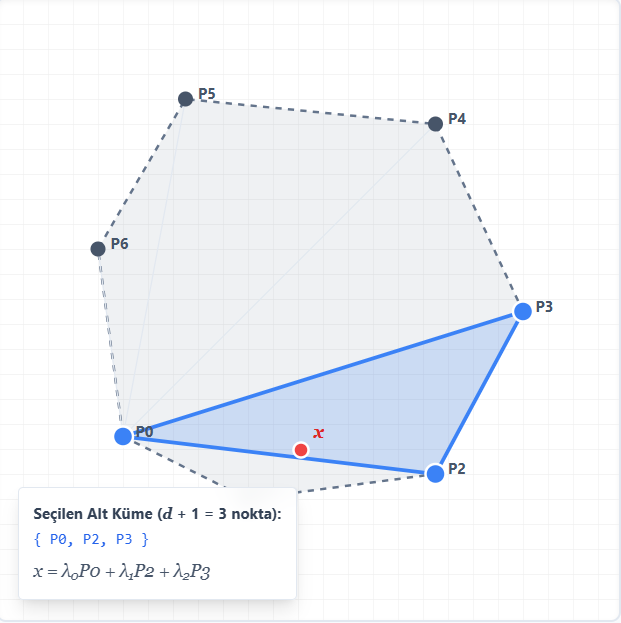
Görselde 2 boyutlu bir durumu görüyorsunuz. Aynı $x$ noktası için birkaç farklı üçgen çizebilirsiniz. Ama önemli olan şu: $x$ nerede olursa olsun, mutlaka onu kapsayan bir üçgen vardır. 3 nokta yeter, daha fazlasına gerek yok.
İspat: Lineer Cebirle Oynuyoruz
İspat gayet zarif aslında. Temelde şunu diyoruz: “Eğer sen bir noktayı 50 tane noktayla ifade ediyorsan, ben sana bu sayıyı nasıl düşüreceğini göstereyim.”
Diyelim Fazladan Noktamız Var
$x \in \text{conv}(P)$ olsun ve biz de onu $k$ tane noktanın karışımı olarak yazmış olalım:
\[x = \sum_{i=1}^k \lambda_i p_i, \quad \sum_{i=1}^k \lambda_i = 1, \quad \lambda_i > 0\]Eğer $k \le d+1$ ise işimiz zaten bitti. Peki ya $k > d+1$ ise? O zaman bu listeyi kısaltabiliriz.
Lineer Bağımlılık Oyunu
$k > d+1$ olduğuna göre, $d$ boyutlu uzayda elimizde çok fazla nokta var. Bir tanesini ($p_1$) referans alalım, diğerlerini ona göre vektör olarak yazalım:
\[v_2 = p_2 - p_1, \quad v_3 = p_3 - p_1, \quad \ldots, \quad v_k = p_k - p_1\]Toplam $(k-1)$ vektör var. Ama bu sayı $d$’den büyük. Demek ki lineer cebirden bildiğimiz bir şey devreye giriyor: $d$ boyutlu uzayda $d$’den fazla vektör lineer bağımlı olmak zorunda. Yani hepsi sıfır olmayan $\mu_2, \ldots, \mu_k$ sayıları vardır ki:
\[\sum_{i=2}^k \mu_i (p_i - p_1) = 0\]Açalım:
\[\sum_{i=2}^k \mu_i p_i - \left(\sum_{i=2}^k \mu_i\right) p_1 = 0\]$\mu_1 = -\sum_{i=2}^k \mu_i$ dersek:
\[\sum_{i=1}^k \mu_i p_i = 0 \quad \text{ve} \quad \sum_{i=1}^k \mu_i = 0\]Bir Noktayı Atıyoruz
Şimdi elimizde iki denklem var:
- $x = \sum_{i=1}^k \lambda_i p_i$
- $0 = \sum_{i=1}^k \mu_i p_i$
İkincisini bir $\alpha$ ile çarpıp birinciden çıkaralım:
\[x = \sum_{i=1}^k (\lambda_i - \alpha \mu_i) p_i\]Akıllıca bir $\alpha$ seçersek, katsayılardan birini tam sıfır yapabiliriz:
\[\alpha = \min_{\mu_i > 0} \frac{\lambda_i}{\mu_i}\]Bu seçimle:
- Minimumu veren katsayı sıfır olur
- Diğerleri pozitif kalır
- Toplamları hâlâ 1
Böylece $x$’i $(k-1)$ nokta ile yazdık! Bu işlemi $k \le d+1$ olana kadar devam ettiririz.
İspat bitti. $\blacksquare$
Peki Niye Önemli?
Şunu düşünün: Türkiye haritası var, sınırları tanımlayan binlerce GPS koordinatı. Siz Ankara’dasınız ve konumunuzu bildirmek istiyorsunuz. Normal şartlarda “Abi binlerce noktanın ortasında bir yerdeyim” demeniz lazım. Ama Carathéodory diyor ki: “Yok canım, 3 tane referans noktası ver bana, yeter. İzmir, Antalya, Trabzon deyin, ben seni bulayım.”
Karmaşık veri kümelerinde bir noktayı tanımlamak için tüm veriyi taşımanıza gerek yok. Boyuta bağlı sabit sayıda “temel nokta” yeter.
Gerçek Dünyada Nerede Kullanılıyor?
Lineer Programlama
Simplex algoritması diye bir şey var, optimizasyon problemlerini çözer. Çözüm uzayının her yerini aramak yerine, sadece köşeler arasında yürür. Carathéodory sayesinde biliyoruz ki optimal çözüm zaten az sayıda “aktif kısıt” tarafından belirleniyor. Gerisi boş iş.
Bilgisayar Ekranları
Şu an bu yazıyı okuduğunuz ekrandaki her renk, Kırmızı, Yeşil ve Mavi ışığın bir karışımı. Bu Carathéodory’nin bir sonucu: 2 boyutlu renk uzayında her renk 3 temel rengin ($2+1$) karışımı. Monitör üreticileri bu yüzden sadece RGB kullanıyor.
Machine Learning
Support Vector Machine (SVM) diye bir algoritma var. Karar sınırını sadece “destek vektörleri” belirler. Veri kümenizdeki binlerce noktanın çoğu aslında gereksiz. Carathéodory’nin ruhu bu: Kritik, ekstrem noktalara odaklan, gerisi önemsiz.
Ekonomi ve Oyun Teorisi
Nash dengesi hesaplarken, sonsuz strateji olsa bile denge noktası sınırlı sayıda “saf strateji”nin karışımıyla ifade edilebilir.
Son Söz
Carathéodory bize şunu öğretiyor: Karmaşıklığın içinde her zaman basit bir iskelet vardır. Çok boyutlu uzaylarda kaybolmamızı engelleyen bir pusula gibi. Bir noktanın kim olduğunu tüm kalabalık değil, sadece en yakın $d+1$ komşusu belirler.
Matematiğin bu “sıkıştırma” teoremleri beni hep büyülemiştir. Sonsuz gibi görünen bir karmaşıklığı alıp sonlu, basit bir yapıya indirgeyebilmek… Bu yüzden konveks geometriyi seviyorum işte.
Kaynakça
- Carathéodory, C. (1911). Über den Variabilitätsbereich der Fourier’schen Konstanten von positiven harmonischen Funktionen. Rend. Circ. Mat. Palermo, 32: 193-217.
- Rockafellar, R. T. (1970). Convex Analysis. Princeton University Press.
- Eckhoff, J. (1993). Helly, Radon, and Carathéodory type theorems. Handbook of Convex Geometry, North-Holland, Amsterdam, 389-448.
- Grünbaum, B. (2003). Convex Polytopes. Springer-Verlag.
Yorumlar