Radon Teoremi: Aslında Bize Ne Anlatıyor?

Matematikte bazen öyle teoremler karşımıza çıkar ki, ilk bakışta “E ne var bunda?” dersiniz ama altını bir kazırsınız, devasa yapılar çıkar! İşte Radon Teoremi tam da böyle bir şey. Konveks geometrinin “Muhteşem Üçlüsü”nden biri sayılan bu teorem (diğer kankaları Helly ve Carathéodory olur), veri kümelerini nasıl parçalayabileceğimize dair bize müthiş bir garanti veriyor.

Gelin, Johann Radon’un ta 1921’de ortaya attığı ve hala başımızın tacı olan bu şık teoreme, şöyle daha samimi bir gözle, görsel sezgilerle bakalım.

Olayın Özü Ne?

Radon Teoremi’ni en sade haliyle şöyle anlatabiliriz: Diyelim ki $d$-boyutlu bir uzaydasınız ($\mathbb{R}^d$). Elinizde $d+2$ tane nokta var. Radon diyor ki; siz bu noktaları iki ayrı takıma ($A$ ve $B$) öyle bir bölersiniz ki, bu iki takımın konveks zarfları (yani onları saran hayali lastik bantlar) mutlaka ama mutlaka birbirine değer! [1]

Matematiğe dökersek; $P = {p_1, \dots, p_{d+2}}$ diye bir nokta kümeniz olsun. Bunu öyle bir $A$ ve $B$ diye ayırıyoruz ki:

Buradaki “konveks zarf”ı, noktaları içine hapseden en küçük dışbükey şekil gibi düşünün. Hani mantar panodaki iğnelerin etrafına lastik geçirirsiniz ya, aynen o!

Gözümüzde Canlandıralım: 2 Boyutta Durum Ne?

Teoremi anlamanın en kestirme yolu, görseldeki gibi düzleme ($\mathbb{R}^2$) bakmak. Düzlemde $d=2$ olduğuna göre, teorem bize 4 nokta ($d+2$) ile kaçışın olmadığını, illa ki bir kesişim yakalayacağımızı söylüyor.

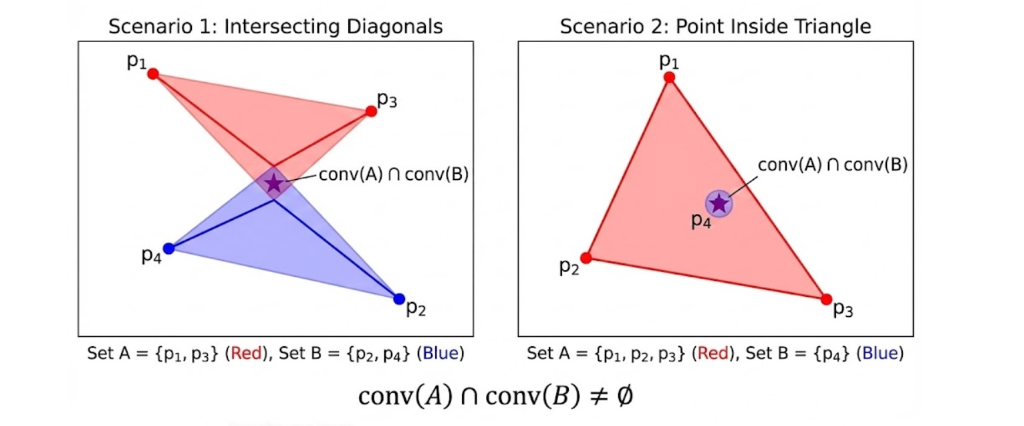
Düzlemdeki 4 nokta için topu topu iki senaryo var zaten [2]:

• Senaryo 1: Kesişen Köşegenler (Intersecting Diagonals): Noktalar bir dörtgen oluşturuyorsa, karşılıklı köşeleri birleştiren köşegenler ortada kesişir. Görseldeki gibi Kırmızı Takım $A={p_1, p_3}$ ve Mavi Takım $B={p_2, p_4}$ olsun. Bu iki doğru parçasının (konveks zarfların) kesişimi, ortadaki mor yıldızdır.
• Senaryo 2: Üçgenin İçindeki Nokta (Point Inside Triangle): Noktalardan biri, diğer üçünün oluşturduğu üçgenin içinde kalıyorsa durum daha da basittir. Kırmızı Takım $A={p_1, p_2, p_3}$ bir üçgen oluşturur, Mavi Takım $B={p_4}$ ise tek bir noktadır. $p_4$ noktası üçgenin içinde olduğu için, kesişim kümesi bizzat $p_4$’ün kendisidir.

Gördüğünüz gibi, Radon Teoremi aslında bir “kaçınılmaz son” hikayesi; o kesişim illa ki olacak!

İşin Mutfağı: Biraz Sayılara Bakalım

Radon Teoremi sadece güzel bir çizimden ibaret sanmayın, arkasında kapı gibi lineer cebir var. Kural şu: $d$ boyutlu uzayda $d+2$ tane vektör varsa, bunlar matematiksel olarak bağımlıdır.

Yani türkçesi şu: Öyle katsayılar ($\alpha_i$) bulabiliriz ki, hepsini toplayınca sıfır eder.

Burada yapacağımız tek numara, katsayıları gruplara ayırmak:

• Artı olanlar ($\alpha_i \ge 0$) $A$ takımına,
• Eksi olanlar ($\alpha_i < 0$) $B$ takımına!

İşte bu basit cebirsel numara, bize o geometrik kesişimi hediye ediyor [3].

Peki Bu Ne İşimize Yarayacak?

Radon Teoremi, kendisinden sonra gelen çok daha karmaşık ve havalı teorilerin babası sayılır:

• Tverberg Teoremi: Radon’un biraz daha gelişmiş versiyonu. Radon noktaları 2 gruba ayırırken, Tverberg “Elini korkak alıştırma, yeterince nokta varsa $r$ tane kesişen gruba da ayırırız” diyor.
• Helly Teoremi: Kümelerin kesişimiyle ilgili meşhur bir teorem var, işte onun ispatı genelde bizim Radon sayesinde yapılıyor.
• Veri Bilimi ve İstatistik: Çok boyutlu verilerin “tam ortasını” bulmak (Centerpoint) veya veriyi “dilimlemek” (Ham-Sandwich Teoremi - ismi harika değil mi?) gibi işlerde hep bu temel mantık kullanılıyor [2].

Son Söz

Uzun lafın kısası, Radon Teoremi bize konveksliğin derin yapısını gösteriyor: Nokta sayısı çok az bile olsa ($d+2$ kadar), geometrik şekiller birbirine dolaşmaya, kesişmeye mecbur. Kaçış yok! Bu “kaçınılmazlık”, modern geometrinin ve veri biliminin kalbinde atıyor.

Kaynaklar

[1] Radon, J. (1921). “Mengen konvexer Körper, die einen gemeinsamen Punkt enthalten.” Mathematische Annalen, 83, 113–115. (Olayın başladığı orijinal makale).

[2] Matoušek, J. (2002). Lectures on Discrete Geometry. Springer-Verlag New York. (Bu işin kitabı yazılmış, Bölüm 1.3’e bakabilirsiniz).

[3] Eckhoff, J. (1993). “Helly, Radon, and Carathéodory type theorems.” Handbook of Convex Geometry, Vol A, 389-448. Elsevier.